Asymptotic behavior of nonlocal bistable reaction-diffusion equations

Summary

We study the asymptotic behavior of nonlocal bistable reaction-diffusion equations.

Abstract

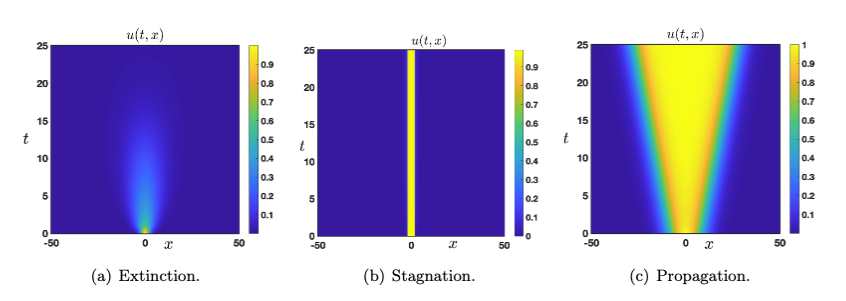
In this paper, we study the asymptotic behavior of the solutions of nonlocal bistable reaction-diffusion equations starting from compactly supported initial conditions. Depending on the relationship between the nonlinearity, the interaction kernel and the diffusion coefficient, we show that the solutions can either: propagate, go extinct or remain pinned. We especially focus on the latter regime where solutions are pinned by thoroughly studying discontinuous ground state solutions of the problem for a specific interaction kernel serving as a case study. We also present a detailed numerical analysis of the problem.

Link to the paper

Recommended citation:

@article{besse2022asymptotic,
title = {Asymptotic behavior of nonlocal bistable reaction-diffusion equations},
journal = {Discrete and Continuous Dynamical Systems - B},
volume = {28},
number = {12},
pages = {5967-5997}
year = {2023},
issn = {1531-3492},
doi = {10.3934/dcdsb.2022211},
url = {https://www.aimsciences.org/article/id/6359d0886aa93c57bccf00ab},
author = {Christophe Besse and Alexandre Capel and Grégory Faye and Guilhem Fouilhé},
keywords = {Nonlocal coupling, pinning phenomena, threshold of propagation}
}